스크린 공간에서 월드 공간으로! 레이 트레이싱을 활용한 구체 충돌 구현
스크린 공간에서 월드 공간으로! 레이 트레이싱을 활용한 구체 충돌 구현
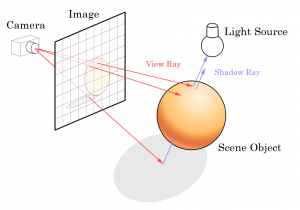
🖼️ 전체 흐름
- 스크린 상의 각 픽셀에서 월드 좌표계 기준으로 Ray를 발사
- 구체와의 충돌 여부 계산
- 충돌했다면, 깊이(hit distance)를 기반으로 색상을 표현하여 입체감을 부여
📦 핵심 구조
✨ Ray 구조체
struct Ray {
vec3 start; // 시작 지점
vec3 dir; // 정규화된 방향 벡터
};
✨ Hit 구조체
struct Hit {
float d; // 충돌 지점까지의 거리 (음수면 충돌 없음)
vec3 point; // 충돌 지점
vec3 normal; // 충돌 시 표면의 법선 벡터
};
🔎 구체와 Ray의 충돌 감지
구체와의 충돌은 위키백과의 Line–sphere intersection 공식을 바탕으로 구현합니다.
🔬 충돌 검사 함수
Hit IntersectRayCollision(Ray &ray)
{
Hit hit = Hit{-1.0f, vec3(0.0f), vec3(0.0f)};
const float b = 2.0f * glm::dot(ray.dir, ray.start - this->center);
const float c = glm::dot(ray.start - this->center, ray.start - this->center) - this->radius * this->radius;
const float nabla = b * b / 4.0f - c;
if (nabla >= 0.0f) {
const float d1 = -b / 2.0 + sqrt(nabla);
const float d2 = -b / 2.0 - sqrt(nabla);
hit.d = glm::min(d1, d2);
hit.point = ray.start * ray.dir * hit.d;
hit.normal = glm::normalize(hit.point - this->center); // 법선벡터
}
return hit;
}
💡 포인트 정리
- **
b와c**는 이차방정식의 계수 - **
nabla**는 판별식(discriminant) - 판별식이 0 이상이면 충돌이 존재
- 두 충돌 지점 중 작은 값을 사용 (
glm::min(d1, d2))
🎨 렌더링 함수
이제 Ray를 물체에 발사하고 충돌 결과를 바탕으로 색상을 표현합니다.
vec3 traceRay(Ray &ray)
{
const Hit hit = sphere->IntersectRayCollision(ray);
if (hit.d < 0.0f)
{
return vec3(0.0f); // 충돌 없음: 검정색
}
return sphere->color * hit.d; // 깊이에 비례해 색상 강도 조절
}
- 충돌 없을 경우: 배경색 반환 (검정)
- 충돌할 경우: 구체의 색상에 깊이(hit distance)를 곱하여 거리감 표현
